Conjuntos

Conjuntos

2.1 Definición, tipos y cardinalidad.

Un conjunto es la agrupación, clase, o colección de objetos o en su defecto de elementos que pertenecen y responden a la misma categoría o grupo de cosas, por eso se los puede agrupar en el mismo conjunto.

Conjunto Universal

Con el ánimo de evitar confusiones, cuando definimos un conjunto debemos especificar de donde se están tomando los elementos que lo conforman. Esto significa que debe existir una base de la cual tomamos los elementos, esta base sobre el cual trabajamos es llamada conjunto universal. Usaremos siempre la letra UU para representar el conjunto universal.

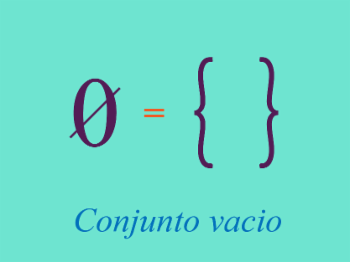
Conjunto vacío
Consideremos la existencia de un conjunto que no tiene elementos, este es llamado conjunto vacío.
Para representar dicho conjunto usamos el reconocido símbolo del vacío

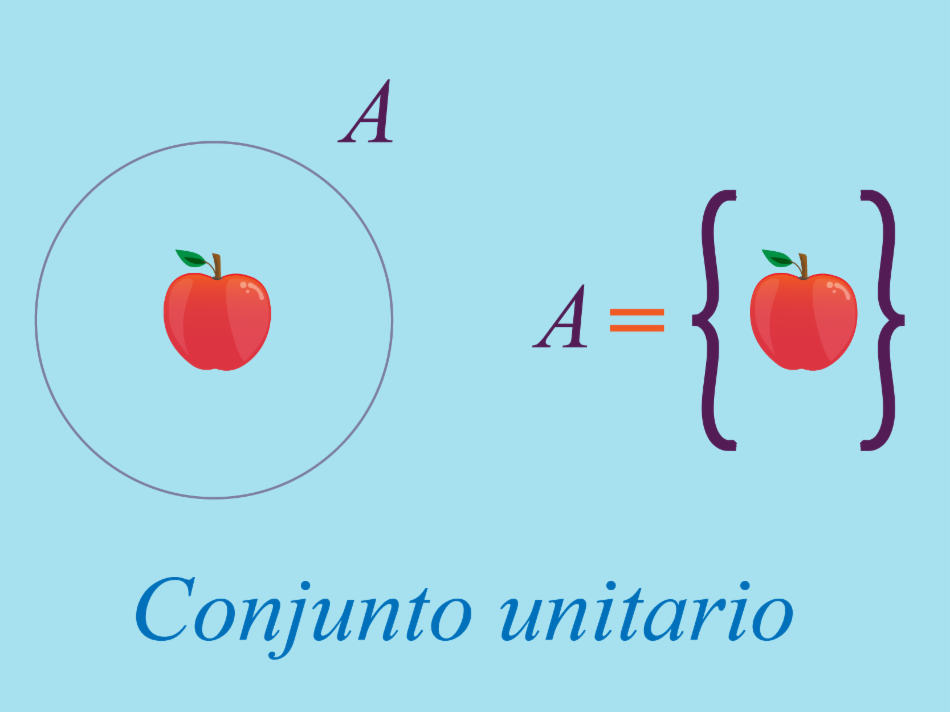
Conjuntos unitarios
El conjunto unitario se distingue por tener solo un elemento. No importa qué tipo de elemento tenga el conjunto, un gato, un perro, un número, una letra, o cualquier otra cosa, si tiene un solo elemento es llamado conjunto unitario.

Conjuntos finitos
Este tipo de conjunto también se distingue por la cantidad de elementos que posee. Un conjunto es finito si podemos contar la cantidad de elementos que lo conforman.

Conjuntos infinitos
No es fácil encontrar en la naturaleza ejemplos de este tipo de conjuntos. Los conjuntos infinitos son aquellos a los cuales no les podemos contar la cantidad de elementos que los componen. El método más fácil para representar este tipo de conjuntos es por comprensión.

En teoría de conjuntos, un número cardinal es una generalización de los números naturales para contar el número de elementos, la cardinalidad, de cualquier conjunto, finito o infinito.

2.2 Cuantificadores
En lógica matemática, teoría de conjuntos y matemáticas en general, los cuantificadores son símbolos utilizados para indicar cuántos o qué tipo de elementos de un conjunto dado cumplen con cierta propiedad (por ejemplo, pertenencia, equivalencia u orden).

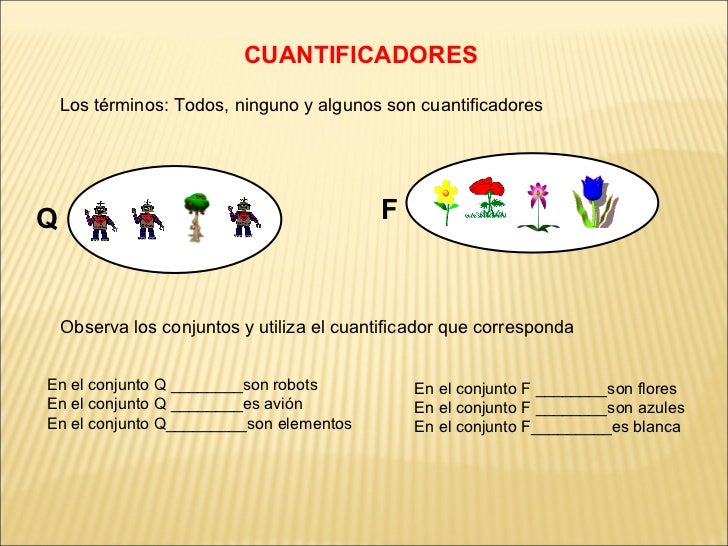
2.3 Operaciones entre conjuntos

Unión de conjuntos

Ejemplos: 

• A={a, b, c, d} y B = {d, e, f} , AUB = {a, b, c, d, e, f}
• A={Juan, Pedro Pablo}, B={María, Martha, Juana}; AUB={Juan, Pedro Pablo, María, Martha, Juana}
• X={cuadrado, triángulo}, Y={círculo, elipse}; XUY = {cuadrado, triángulo, círculo, elipse}
• M={auto, motocicleta}, N={barco, lancha}; MUN={auto, motocicleta, barco, lancha}
• T={martillo, pinzas}, S={desarmador}; TUS = {martillo, pinzas, desarmador}
• D={árbol, palmera, arbusto}, E={planta, flor, fruto}; DUE={árbol, palmera, arbusto, planta, flor, fruto}

Intersección de conjuntos

Ejemplos:

• A={a, b, 1, 2, 3} y B={3, 4}; se tiene que A ∩ B={3}
• A={a, b} y B={a, b, u, v}; se tiene que A ∩ B={a, b}
• A={a, b, c, d, e, f, g} y B={d, e, f, g, h, i}; se tiene que A ∩ B={d, e, f, g}
• A={♠, ♣} y B={♠, ♣, ♦}; se tiene que A ∩ B={♠, ♣}
• A={x, y, ♦, ◊} y B={y, z, ♠, ♣, ♥, ♦, ◊}; se tiene que A ∩ B={y, ♦, ◊}
• A={lunes, martes} y B={martes, viernes, sábado, domingo}; se tiene que A ∩ B={martes}

Diferencia de conjuntos

En este caso se deben seleccionar los elementos de un conjunto que no estén en el otro.

Diferencia simétrica de conjuntos

En esta ocasión se deben escoger los elementos de $M$ que no están en $N$, y los elementos de $N$ que no están en $M$.

Complemento de un conjunto

La última operación que estudiaremos no es entre dos conjuntos.  Decimos que el complemento de $M$ es el conjunto conformado por todos los elementos del conjunto universal $U$, que no pertenecen al conjunto $M$

$M$

2.5 Relaciones

Relación de pertenencia

Para comenzar, debes comprender la relación entre los conjuntos y los elementos que lo conforman. Cuando un objeto es uno de los elementos de un conjunto decimos que pertenece al conjunto.

Se usa el símbolo que se muestra en la figura de la izquierda como el símbolo de la pertenencia. Si queremos representar que cierto objeto no pertenece a determinado conjunto usaremos el mismo símbolo atravesado por una línea

Relación de contenencia y subconjuntos

Definamos como F y G los conjuntos que se muestran en el siguiente diagrama de Venn:

Como te puedes dar cuenta, cada elemento que pertenece al conjunto G, pertenece también al conjunto F. Cuando se da esta situación decimos que un conjunto está contenido en el otro, o que es un subconjunto del otro.
En este caso G está contenido en F, o lo que es igual, G es subconjunto de F.

Para el caso de los conjuntos F y G definidos anteriormente, la representación correcta es como se muestra en la figura de abajo.

También es posible representar de forma escrita la relación de contenencia entre conjuntos.Se usa el símbolo que se muestra en la figura de la izquierda como el símbolo de la contenencia. Si queremos representar la no contenencia de conjuntos usaremos el mismo símbolo atravesado por una línea como se muestra en la figura.

2.6 Funciones

Es la relación que asocia cada elemento de un primer conjunto con uno y sólo uno de los elementos de un segundo conjunto.