Números Reales
3.1 Conjuntos numéricos
Los números naturales
Con los números naturales contamos los elementos de un conjunto (número cardinal). O bien expresamos la posición u orden que ocupa un elemento en un conjunto (ordinal).
El conjunto de los números naturales está formado por:
N= {0, 1, 2, 3, 4, 5, 6, 7, 8, 9,...}
La raíz de un número natural no siempre es un número natural, sólo ocurre cuando la raíz es exacta.
Son todos número de 0 al +∞
Los números enteros
Los números enteros son del tipo:
Z = {...−5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5 ...}

Nos permiten expresar: el dinero adeudado, la temperatura bajo cero, las profundidades con respecto al nivel del mar, etc.
La suma, la diferencia y el producto de dos números enteros es otro número entero.
Ejemplos:
números enteros, estos se dividen en enteros positivos y negativos:
Los números racionales
Se llama número racional a todo número que puede representarse como el cociente de dos enteros, con denominador distinto de cero.


Ejemplos:
Los números irracionales
Un número es irracional si posee infinitas cifras decimales no periódicas, por tanto no se pueden expresar en forma de fracción.
El número irracional más conocido es , que se define como la relación entre la longitud de la circunferencia y su diámetro.
, que se define como la relación entre la longitud de la circunferencia y su diámetro.
 = 3.141592653589...
= 3.141592653589...
Otros números irracionales son:
El número e aparece en procesos de crecimiento, en la desintegración radiactiva, en la fórmula de la catenaria, que es la curva que podemos apreciar en los tendidos eléctricos.
e = 2.718281828459...
El número áureo, , utilizado por artistas de todas las épocas (Fidias, Leonardo da Vinci, Alberto Durero, Dalí,..) en las proporciones de sus obras.
, utilizado por artistas de todas las épocas (Fidias, Leonardo da Vinci, Alberto Durero, Dalí,..) en las proporciones de sus obras.

√99: 9.94987437107
√685: 26.1725046566
√189: 13.7477270849
√7: 2.64575131106
√286: 16.9115345253
√76: 8.71779788708
Números reales
 Con los números reales podemos realizar todas las operaciones, excepto la radicación de índice par y radicando negativo y la división por cero.
Con los números reales podemos realizar todas las operaciones, excepto la radicación de índice par y radicando negativo y la división por cero.
Ejemplos:
- 0
- 1
- 2
- 3
- 4
- 5....
Los números enteros
Los números enteros son del tipo:
Z = {...−5, −4, −3, −2, −1, 0, 1, 2, 3, 4, 5 ...}
Nos permiten expresar: el dinero adeudado, la temperatura bajo cero, las profundidades con respecto al nivel del mar, etc.
La suma, la diferencia y el producto de dos números enteros es otro número entero.
Ejemplos:
- -1
- -2
- -3
- -4
- -5
- 0
- 1
- 2.....
Los números racionales
Se llama número racional a todo número que puede representarse como el cociente de dos enteros, con denominador distinto de cero.
Ejemplos:
- 0.1
- 0.25
- 0.5
- 2/3
- 4/7
- 9/10
Los números irracionales
Un número es irracional si posee infinitas cifras decimales no periódicas, por tanto no se pueden expresar en forma de fracción.
El número irracional más conocido es
Otros números irracionales son:
El número e aparece en procesos de crecimiento, en la desintegración radiactiva, en la fórmula de la catenaria, que es la curva que podemos apreciar en los tendidos eléctricos.
e = 2.718281828459...
El número áureo,
Ejemplos:
El conjunto formado por los números racionales e irracionales es el conjunto de los números reales, se designa por  .
.
Números imaginarios
Un número imaginario se denota por bi, donde :
b es un número real
i es la unidad imaginaria: 
Los números imaginarios permiten calcular raíces con índice par y radicando negativo.
x2 + 9 = 0
Un número complejo en forma binómica es a + bi.
El número a es la parte real del número complejo.
El número b es la parte imaginaria del número complejo.
Si b = 0 el número complejo se reduce a un número real, ya que a + 0i = a.
Si a = 0 el número complejo se reduce a bi, y se dice que es un número imaginario puro.
El conjunto de los números complejos se designa por
3.2 Operaciones entre números reales
Adición de Números Reales
En la adición de números reales, los términos que intervienen son los sumandos y el resultado, donde el orden de los sumandos no altera el resultado.
Sustracción de Números Reales
Pero al multiplicar dos factores con signo negativo, el cambio se dará bajo la regla de:
−⋅−=+
Por lo tanto, si tenemos dos factores con signo negativo, la regla sería.
Si se calcula dos factores, ambos con signo diferente, uno positivo y otro negativo, entonces la respuesta va a ser negativa.
Al operar con varios factores de signos variados, se debe contar la cantidad de factores con signo negativo. Si hay un número par, el resultado es positivo. Si hay un número impar, el resultado es negativo.
Si se multiplica por cero, el resultado será cero.
División de números Reales
Sin embargo, la división solo se puede realizar entre números mayores o menores que cero, mas no el mismo cero, ya que el resultado no está definido en estos casos.
Potenciación de números Reales
a0=1
Potencia de potencia.
RELACIONES DE ORDEN DE LOS NÚMEROS REALES
Para contar siempre llevamos un orden, 1 después el 2, luego el 3 y luego el 4.
La correspondencia uno a uno entre el conjunto de los números reales y los puntos de una recta numérica permite representar geométricamente la relación de orden de los números reales, según la cual los números reales son ordenados.
Si a y b son números reales, entonces se tiene lo siguiente:
a > b , a < b , o bien a = b
Esta propiedad recibe el nombre de ley de tricotomía.

Expresión Algebraica Irracional: Es irracional cuando las variables están afectadas por la radicación


Ejemplos:

Fraccionaria
Una expresión algebraicas racional es fraccionaria cuando la indeterminada aparece en algún denominador.

Ejemplos:

3.5 Razones y proporciones
Razón
Una razón es una comparación entre dos o más cantidades. Puede expresarse mediante una fracción. Si las cantidades a comparar son a y b, la razón entre ellas se escribe como:




28 / 7
Proporción
36:9::28:7
15 / 3
Proporción
35:7::15:3
21 / 3
Proporción
14:2::21:3
45 / 5
Proporción
15:3::45:5
El valor absoluto puede ser explorado ya sea numérica o gráficamente. Numéricamente, el valor absoluto se indica encerrando el número, variable o expresión dentro de barras verticales, así:
Cuando tomamos el valor absoluto de un número, éste es siempre positivo o cero. Si el valor original ya es positivo o cero, el valor absoluto es el mismo. Si el valor original es negativo, simplemente nos deshacemos del signo. Por ejemplo, el valor absoluto de 5 es 5. El valor absoluto de -5 es también 5.
En cuanto a las matemáticas, las ecuaciones de primer grado son la introducción al álgebra. Su comprensión es imprescindible para cualquier tipo de ecuaciones: ecuaciones de segundo grado o de grado mayor, exponenciales, irracionales, etc. y para los sistemas de ecuaciones.
En cuanto a la vida real, aunque en un principio no se piense así, las ecuaciones son una herramienta de gran utilidad que nos permiten resolver numerosos problemas a los que nos enfrentamos diariamente.
Ejemplos:
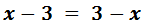
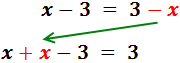
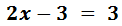
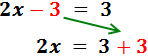
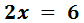
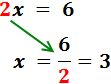
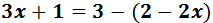
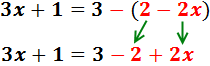
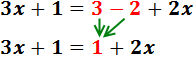
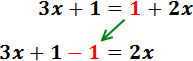
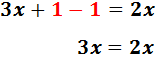
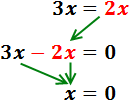
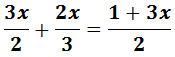
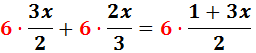
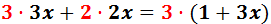
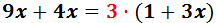
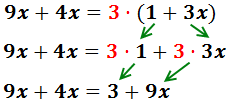
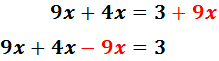
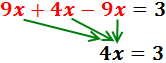
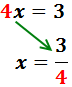
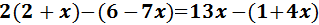
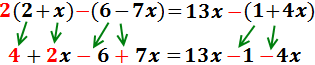
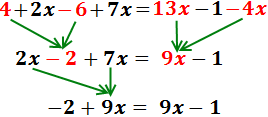
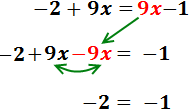
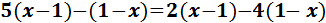
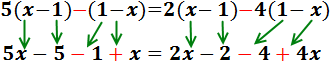
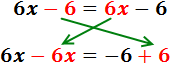
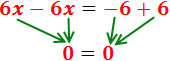
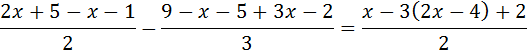
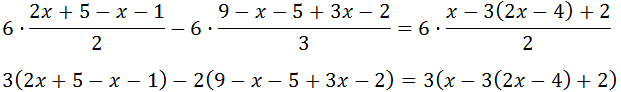
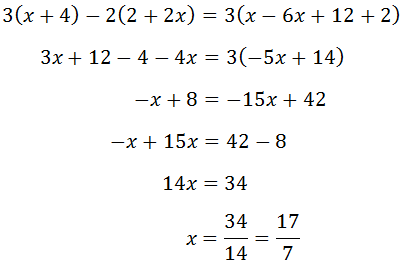
Ejemplo:
La solución de esta inecuación es el intervalo .
Ejemplo:
Esta inecuación no tiene soluciones (reales) puesto que ningún número al cuadrado es negativo.
Ejemplo:
La solución de esta inecuación es .
Ejemplo:
Esta inecuación no tiene solución porque el módulo (valor absoluto) de un número es siempre mayor o igual que 0.
1.
2.
3.
4.
a+b=b+a
al ser, los números reales, un conjunto que incluye los números negativos, la suma de negativos es posible, sin tener que recurrir a otro conjunto de números. Entonces, las sumas se pueden realizar como:
a+(−b)=(−b)+a=−b+a
Por ejemplo, podemos tomar los dos sumandos, 7 y −11. El orden de estos, al sumarlos, no va a alterar el resultado, ya que se trata al sumando como un término en su valor absoluto. Pero si se lo tomara por su valor relativo, no se podría sumar 7+11 o 11+7 y esperar el mismo resultado que:
7+(−11)=−11+7=−4
En este caso, el resultado es negativo, ya que el sumando con valor negativo es mayor que el término con valor positivo.
A pesar de que todas las operaciones de sustracción de
números reales pueden ser expresadas como sumas, como se podía ver en el
ejemplo anterior, también en la sustracción existen reglas para evitar
confusiones. Pues, los términos que intervienen en esta operación, son el
sustraendo, el minuendo y el resultado. El sustraendo siempre va primero, el
minuendo va siempre después, logrando que el orden de los términos si acabe por
afectar al resultado.
a−b≠b−a
Donde a+(−b)si es igual a (−b)+a. Por lo cual, para poder cambiar de orden a
los términos de una resta, se debe usar el inverso aditivo o el negativo del
sustraendo para que de esta manera no se vaya a alterar el resultado.
Multiplicación de números Reales
En la multiplicación de números reales, los términos son los
factores y el producto o resultado. En esta operación, los factores no alteran
el producto, sin embargo, existen otras reglas para multiplicar cuando se
tienen números negativos.
Al multiplicar dos factores con el mismo signo positivo, la
respuesta será la misma multiplicación, sin cambios.
a×b=c
Pero al multiplicar dos factores con signo negativo, el cambio se dará bajo la regla de:
+⋅+=+
+⋅−=−
−⋅+=−
−⋅−=+
Por lo tanto, si tenemos dos factores con signo negativo, la regla sería.
−a×−b=c
Si se calcula dos factores, ambos con signo diferente, uno positivo y otro negativo, entonces la respuesta va a ser negativa.
a×−b=−ca
−a×b=−c
Al operar con varios factores de signos variados, se debe contar la cantidad de factores con signo negativo. Si hay un número par, el resultado es positivo. Si hay un número impar, el resultado es negativo.
a×−b×−c=d
a×−b×c=−d
Si se multiplica por 1, cualquier factor daría como
resultado el mismo factor.
a×1=a
Si se multiplica por cero, el resultado será cero.
a×0=0
En la división de números reales, se aplican las mismas
reglas de signos que en la multiplicación. Y en las fracciones, si uno de los
dos términos tiene signo negativo, toda la fracción se convierte en un número
negativo.
a/−b=−a/b=a/b
Sin embargo, la división solo se puede realizar entre números mayores o menores que cero, mas no el mismo cero, ya que el resultado no está definido en estos casos.
La potenciación tiene varias reglas como:
a0=1
a1=a
Multiplicación y división de potencias con la misma base.
am×an=am+n
am÷an=am−n
Potencia de potencia.
(am)n=am×n
Multiplicación y división de potencias con el mismo exponente.
an×bn=(a×b)n
an÷bn=(a÷b)n
3.3 Relación de orden
RELACIONES DE ORDEN DE LOS NÚMEROS REALES
Para contar siempre llevamos un orden, 1 después el 2, luego el 3 y luego el 4.
La correspondencia uno a uno entre el conjunto de los números reales y los puntos de una recta numérica permite representar geométricamente la relación de orden de los números reales, según la cual los números reales son ordenados.
Si a y b son números reales, entonces se tiene lo siguiente:
- Sia a-b es mayor que cero, es decir , a-b > 0, a es mayor que b, lo que se simboliza con a > b. El símbolo > significa " mayor que".
- Si a - b es menor que cero, entonces a es menor que b, lo que se escribe a < b. El símbolo < significa "menor que".
- Si a - b = 0, entonces a = b
a > b , a < b , o bien a = b
Esta propiedad recibe el nombre de ley de tricotomía.
3.4 Expresiones algebraicas
Trabajar en álgebra consiste en manejar relaciones numéricas
en las que una o más cantidades son desconocidas. Estas cantidades se llaman
variables, incógnitas o indeterminadas y se representan por letras.
Una expresión algebraica es una combinación de letras y
números ligadas por los signos de las operaciones: adición, sustracción,
multiplicación, división y potenciación.
Las expresiones algebraicas nos permiten, por ejemplo,
hallar áreas y volúmenes.
- Longitud de la circunferencia: 2πr, donde r es el radio de la circunferencia.
- Área del cuadrado: S = l2, donde l es el lado del cuadrado.
- Volumen del cubo: V = a3, donde a es la arista del cubo.

Expresión Algebraica Irracional: Es irracional cuando las variables están afectadas por la radicación

En las expresiones algebraicas racionales encontramos dos clases:
Entera
Una expresión algebraicas es racional entera cuando la indeterminada está afectada sólo por operaciones de suma, resta, multiplicación y potencia natural.Ejemplos:
Fraccionaria
Una expresión algebraicas racional es fraccionaria cuando la indeterminada aparece en algún denominador.

Ejemplos:
3.5 Razones y proporciones
Una razón es una comparación entre dos o más cantidades. Puede expresarse mediante una fracción. Si las cantidades a comparar son a y b, la razón entre ellas se escribe como:

Ejemplo:







Proporciones
En una sala de clases hay 10 mujeres y 18 hombres. ¿Qué relación numérica existe entre el número de mujeres y el número de hombres?
La relación entre el número de mujeres y el número de hombres es de "10 es a 18" , otra forma de leerlo es "10 de 18 "
El término a es el antecedente de la razón y el b, el consecuente.

El resultado de la división o cociente entre el antecedente y el consecuente se denomina valor de la razón

Dos o más razones son equivalentes cuando tienen igual valor.
1.1- Resolución de problemas:
Veamos cómo resolver problemas de razones:
Ejemplo 1:
La edad de 2 personas están en la relación de 5 a 9 y la suma de ellas es 84. Hallar las edades.
Solución:
Si las edades son a y b
Cuando nos hablan de relación o razón entre dos cantidades sabemos que nos están hablando de una comparación entre dos cantidades. Por lo tanto expresamos los datos como una razón:

Ahora volvemos a los datos del problema:
Nos indican que la suma de los 2 números nos tiene que dar 84. Esto se expresa así:

Ahora lo que debemos hacer es trabajar con una constante, que en este caso será " X" . Por lo tanto :

Reemplazando los datos en la ecuación tenemos:

Ahora que tenemos el valor de x podemos reemplazar para obtener los valores de a y b :

Respuesta: Por lo tanto podemos decir que las edades son 30 y 54.
Una proporción es la igualdad de dos razones.

2.1- Propiedad fundamental
En toda proporción, el producto de los términos medios es igual al producto de los términos extremos (Teorema fundamental de las proporciones). Es decir:

Ejemplo:
Si tenemos la proporción:

Y le aplicamos la propiedad fundamental señalada queda:
3 • 20 = 4 • 15, es decir, 60 = 60
Esta es la propiedad que nos permite detectar si dos cantidades presentadas como proporción lo son verdaderamente.
Ejemplos de Razones y proporciones:
- Razones
15 / 5
9 / 3
Proporción
15:5::9:3
9 / 3
Proporción
15:5::9:3
- Razones
20 / 4
10 / 2
Proporción
20:4::10:2
10 / 2
Proporción
20:4::10:2
- Razones
28 / 7
Proporción
36:9::28:7
- Razones
15 / 3
Proporción
35:7::15:3
- Razones
21 / 3
Proporción
14:2::21:3
- Razones
45 / 5
Proporción
15:3::45:5
3.6 Valor absoluto
El valor absoluto puede ser explorado ya sea numérica o gráficamente. Numéricamente, el valor absoluto se indica encerrando el número, variable o expresión dentro de barras verticales, así:
|20|
|x|
|4n − 9|
Cuando tomamos el valor absoluto de un número, éste es siempre positivo o cero. Si el valor original ya es positivo o cero, el valor absoluto es el mismo. Si el valor original es negativo, simplemente nos deshacemos del signo. Por ejemplo, el valor absoluto de 5 es 5. El valor absoluto de -5 es también 5.
Ejemplo
| |
Valor
|
Valor
Absoluto
|
5
|
5
|
-5
|
5
|
Recuerda, en situaciones de valor absoluto no estamos cambiando la posición ni la dirección de un número, sólo estamos ignorando esos detalles.
Ten cuidado de no confundir las |barras de valor absoluto| con los (paréntesis) o los [corchetes]. No son los mismos símbolos, y las reglas que los evalúan son diferentes.
Por ejemplo, -1(-3) = 3. Los signos negativos dentro y fuera de los paréntesis se cancelan cuando son multiplicados.
Ejemplo
| |||
Problema
|
-1(-3)
|
=
| |
-1 • -3
|
=
|
3
| |
Pero -1|-3| = -3. No puedes multiplicar a través de las barras de valor absoluto, por lo que primero tienes que encontrar el valor absoluto del número contenido entre ellas. Como el valor absoluto de -3 es 3, la operación se convierte en -1(+3).
Ejemplo
| |||
Problema
|
-1|-3|
|
=
| |
-1 • 3
|
=
|
-3
| |
Cuando las barras de valor absoluto contienen una expresión que incluye operaciones, la expresión debe ser evaluada antes de encontrar el valor absoluto. Considera la expresión |6 − 4|. Antes de que podamos obtener el valor absoluto de la expresión, tenemos que efectuar la resta. Cuando hacemos eso, |6 − 4| se convierte |2|. Ahora podemos calcular el valor absoluto de la expresión — es el valor absoluto de 2, el cual es 2.
|6 − 4| = |2| = 2
De manera similar, para la expresión |15 − 21|, debemos realizar primero las operaciones dentro de las barras de valor absoluto.
|15 − 21| = |-6| = 6
Ejemplos:
- /+10/=10
- /-9/=9
- /-3/=3
- /-34/=34
- /+1300/=1300
- /+123/=123
3.7 Ecuaciones
En cuanto a la vida real, aunque en un principio no se piense así, las ecuaciones son una herramienta de gran utilidad que nos permiten resolver numerosos problemas a los que nos enfrentamos diariamente.
Ejemplos:
Ecuación I.1: ecuación básica
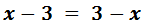
Pasamos las x's a un lado de la igualdad (izquierda) y los números al otro lado (derecha):
En la derecha, la x está restando. Pasa a la izquierda sumando:
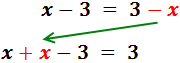
Sumamos los monomios con x’s:
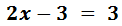
En la izquierda, el -3 está restando. Pasa a la derecha sumando:
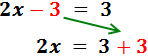
Sumamos los monomios de la derecha:
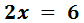
El coeficiente de la x es 2. Este número está multiplicando a x, así que pasa al otro lado dividiendo:
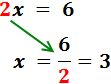
Por tanto, la solución de la ecuación es x = 3.
Ecuación I.2: ecuación con paréntesis
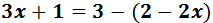
Recordamos que los paréntesis sirven para agrupar elementos, para simplificar o para evitar ambigüedades.
El signo negativo de delante del paréntesis indica que los monomios que contiene tienen que cambiar de signo:
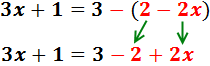
Sumamos 3 y -2 en el lado derecho:
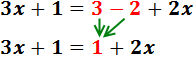
Pasamos los monomios con x’s a la izquierda y los números a la derecha:
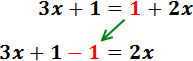
Sumamos 1 y -1. Como el resultado es 0, no lo escribimos:
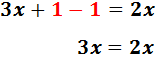
Pasamos 2x a la izquierda restando y sumamos los monomios:
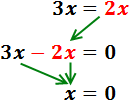
Luego la solución de la ecuación es x = 0.
Ecuación I.3: ecuación con fracciones
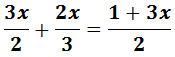
Tenemos varias formas de proceder con las fracciones:
- Sumar las fracciones de forma habitual.
- Multiplicar la ecuación por el mínimo común múltiplo de los denominadores.
En esta ecuación aplicaremos la segunda opción. De este modo los denominadores van a desaparecer.
Multiplicamos, pues, por m.c.m.(2, 3) = 6:
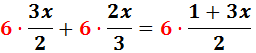
Para simplificar, calculamos las divisiones:
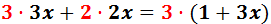
Nótese que hemos escrito un paréntesis al eliminar la fracción de la derecha. Esto se debe a que el 3 debe multiplicar al numerador que está formado por una suma.
Calculamos los productos:
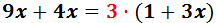
Para eliminar el paréntesis, multiplicamos por 3 todos los elementos que contiene:
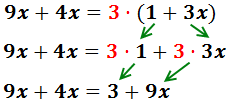
Pasamos las x’s a la izquierda:
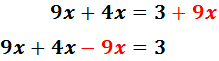
Sumamos los monomios:
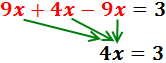
Finalmente, el coeficiente de la x pasa dividiendo al otro lado:
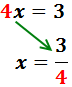
La solución de la ecuación es x = 3/4.
La fracción no se puede simplificar más puesto que ya es irreductible (el máximo común divisor del numerador y del denominador es 1).
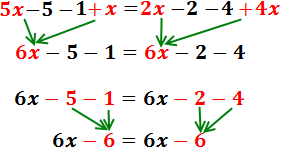
Ecuación I.4: ecuación sin solución
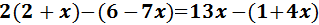
Eliminamos los paréntesis:
El de la izquierda tiene un 2 delante, por lo que multiplicamos su contenido por 2.
Los otros dos paréntesis tienen un signo negativo delante, así que cambiamos los signos de sus monomios:
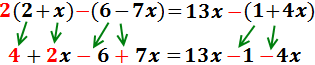
Para simplificar, en cada lado sumamos los monomios con y sin parte literal (los que tienen xy los que no):
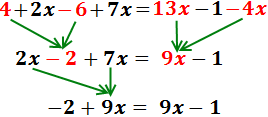
Pasamos las x’s al lado izquierdo y sumamos:
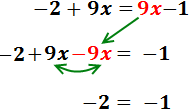
Hemos obtenido una igualdad falsa: -2 = -1. Esto significa que la ecuación nunca se cumple, sea cual sea el valor de x. Por tanto, la ecuación no tiene solución.
Ecuación I.5: ecuación con infinitas soluciones
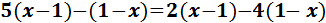
Eliminamos los paréntesis multiplicando sus sendos contenidos por el número que tienen delante. No
hay que olvidar que si el número de delante es negativo, también hay que cambiar los signos:
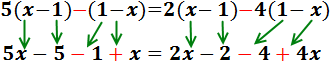
En cada lado, sumamos los monomios según su parte literal:

Pasamos las x’s a la izquierda y los números a la derecha:
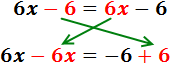
Sumamos los monomios:
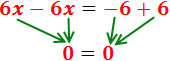
Hemos obtenido una igualdad que siempre se cumple: 0 = 0. Esto significa que la ecuación se cumple siempre, independientemente del valor de x.
Por tanto, la ecuación tiene infinitas soluciones (x puede ser cualquier número y hay infinitos números).
Podemos expresarlo como “x es cualquier real”:
Ecuación III
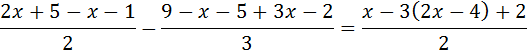
Multiplicamos toda la ecuación por el mínimo común múltiplo de los denominadores: 6
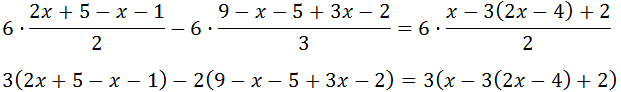
Eliminamos los paréntesis:
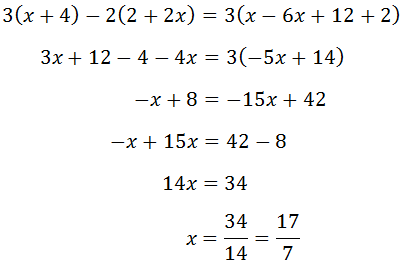
3.8 Inecuaciones
Inecuación lineal: cuando las expresiones de ambos lados son polinomios de primer grado.
Ejemplo:
Inecuación de segundo grado: cuando las expresiones de ambos lados son polinomios de grado menor o igual que 2.
Ejemplo:
Inecuación racional: cuando las expresiones de uno o ambos lados son un cociente de polinomios.
Ejemplo:
Inecuación con valor absoluto: cuando en las expresiones algebraicas hay valores absolutos.
Ejemplo:
Ejemplos:






No hay comentarios:
Publicar un comentario